Cordic Ipの使い方 抑えるべきポイントと注意点 ひがし研究所
アークタンジェントとは、そのタンジェントが 数値 となる角度のことです。 戻り値の角度は、pi/2 ～ pi/2 の範囲内のラジアンで示されます。計算誤差が少ない． 座標が整数ならば，外積も整数演算ですむ．その場合計算誤差は0．(ただしオーバーフローに注意) 逆三角関数では角度に不連続点があるので， 2つの角度を比較しようとすると場合分けが必要で，処理が複雑になる．
Tan 角度 計算 エクセル
Tan 角度 計算 エクセル-エクセル 三角関数計算 ・三角関数の計算を行うエクセルソフトです。 ・このサイトのウェブアプリケーション「直角三角形」 「一般の三角形」 「2点（4点）の座標から角度を算出」と同じものをエクセルで使えるようにしました。角度のsinを返す サイン =SIN(ラジアン) 角度のcosを返す コサイン =COS(ラジアン) 角度のtanを返す タンジェント =TAN(ラジアン) 度数とラジアン;
エクセルを用いた虚数 複素数計算
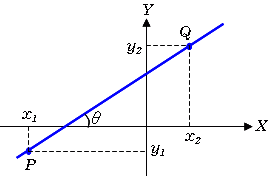
計算 底辺 (a) 高さ (h) 斜辺 (b) 角度 (θ) 面積 (S) 2500 続いてこれらの座標間の角度を上と同じ要領で計算してみましょう。 具体的にはセルに=degrees(atan(d2))と入れればいいです。 こちらもenterにて確定、オートフィルで処理します。 最後にこれらの角度の差をとれば、3点の座標から角度を計算することができます。25/5/ Excelで平方根を計算する方法は以下の3つがあります。お好みの方法をお使いください。 SQRT関数を使う方法 SQRT（スクエア・ルート）関数は、数値の正の平方根を返す関数です。SQRT関数を使ってExcelで平方根を計算する手順は以下の通りです。 作業時間：1分
ASIN 関数 を使用すると、サインから角度を計算することができます。 サインは、直角三角形の斜辺に対する対辺の比のことで、「対辺の長さ÷斜辺の長さ」になります。 =ASIN (対辺の長さ/斜辺の長さ) 上の 関数 の計算結果はラジアンになります。 そこで、 DEGREES 関数 を使ってラジアンを角度に変換します。 =DEGREES (ASIN (対辺の長さ/斜辺の長さ)) 「対辺の長さ角度が度で表されている場合は、角度に PI ()/180 を掛けるか、または RADIANS 関数を使用して角度をラジアンに変換します。14/7/21 底辺と高さから角度と斜辺を計算 男/40歳代/その他/非常に役に立った/ 膝が悪い親が階段のリフォームに言及していたため、情報収集として、階段のサイズや角度を計算するために利用しました。 男/歳未満/小・中学生/役に立った/ あるTwitterでの友達が家からの景色をツイートしていたためそれを特定するためにとった角度や太陽の角度を測った。 男/50歳
Tan 角度 計算 エクセルのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 | Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 | Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |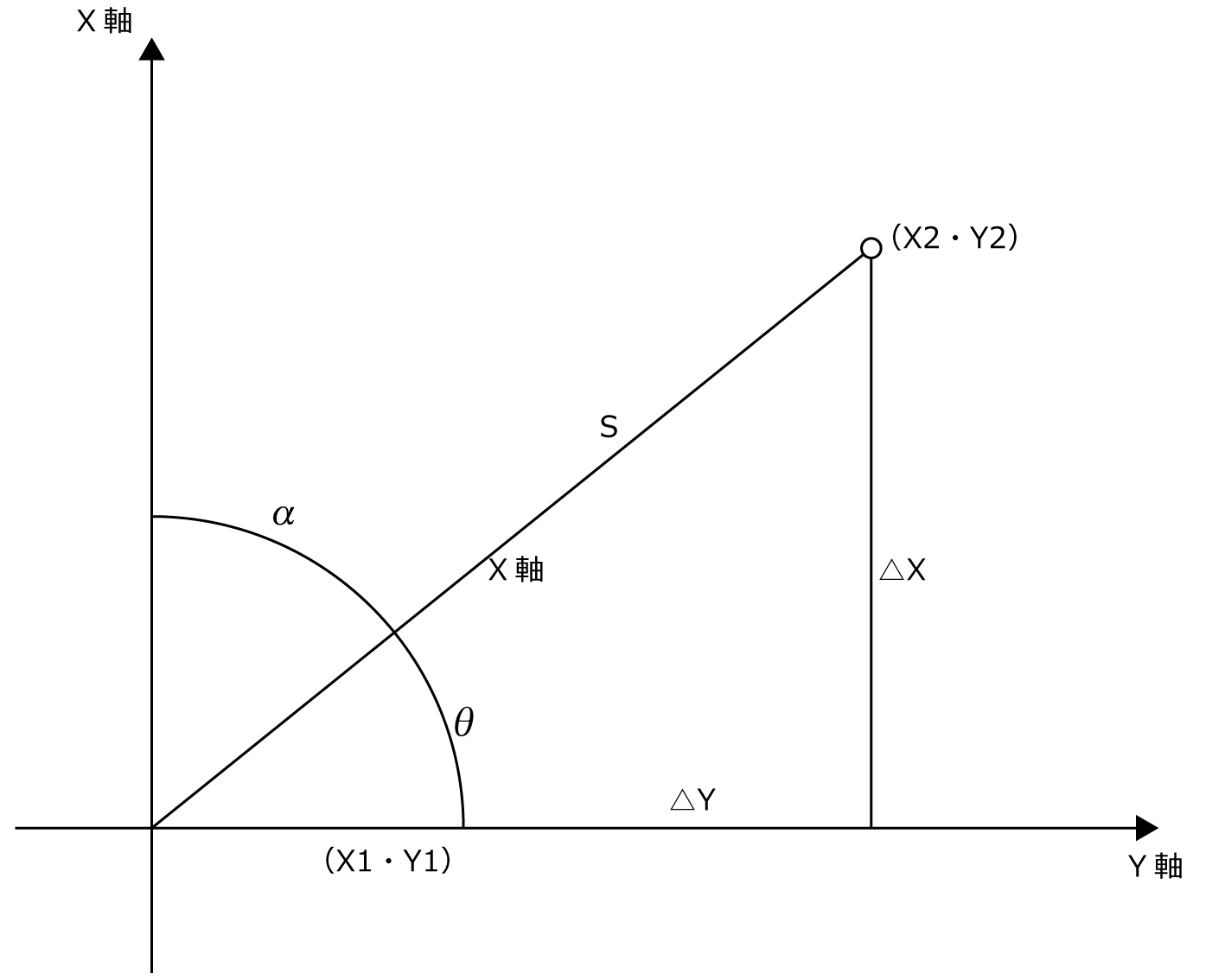
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 | Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 | 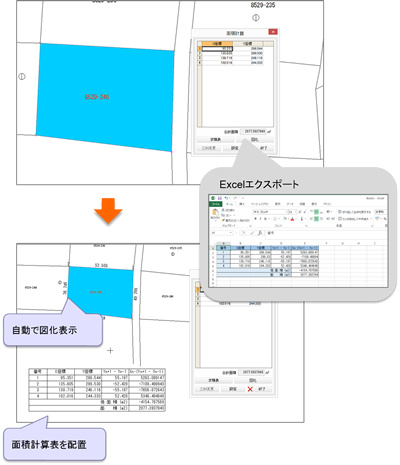 Excelを用いたベクトルの計算 | Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 | 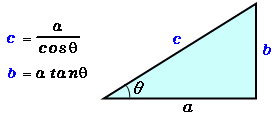 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 | 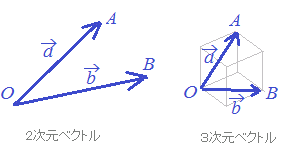 Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 | 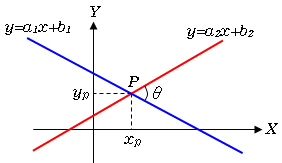 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 | Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 | 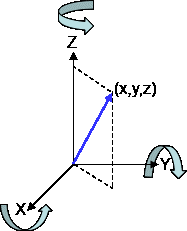 Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 | 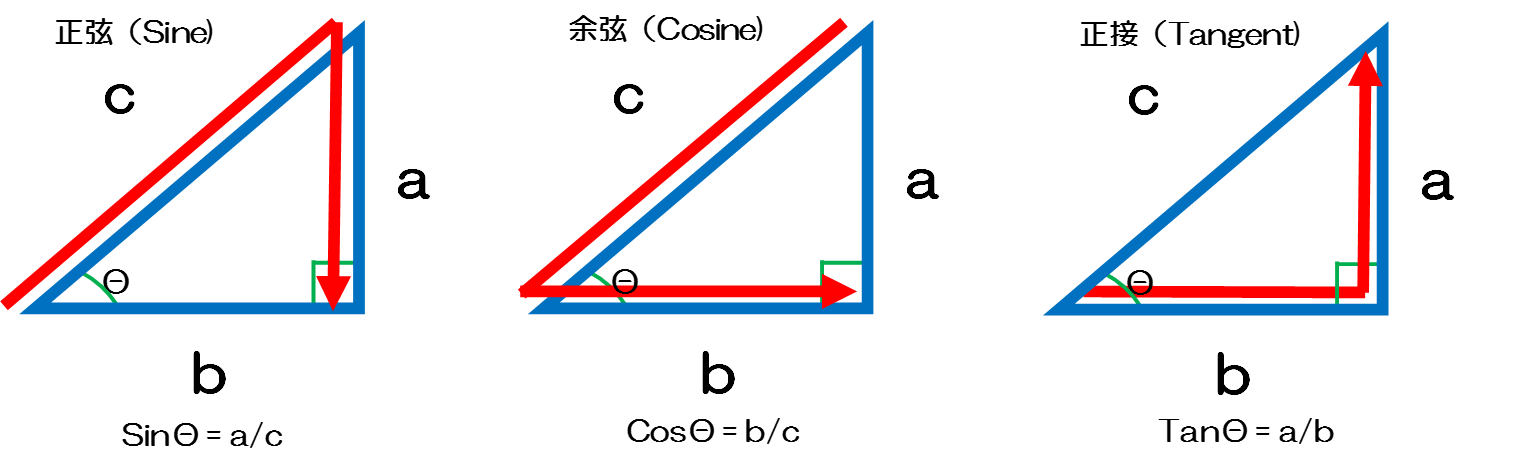 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |  Excelを用いたベクトルの計算 |
 Excelを用いたベクトルの計算 | Excelを用いたベクトルの計算 |
0°01′00″表示の場合、正しく計算できていませんでした。 5/17分を削除致します。 Excelで三角関数（sin,cos,tan)を利用する場合、角度（度分秒）を ラジアンに変換しなければいけません。 たとえば 60度30分36秒の場合、1度＝60分、1度＝3600秒ですので斜辺と高さから計算した角度に×180/πを実行します。 先ほどと同様にπはエクセル上では、PI関数を使用します。 Enterで計算を確定させると、斜辺と高さから角度を計算することができるのです。 関連記事 エクセルで三角関数の計算を行う方法
Incoming Term: エクセル 角度 計算, エクセル 角度 計算 ラジアン, エクセル 角度 計算方法, エクセル 角度 度分秒 計算, エクセル コサイン 角度 計算, エクセル 三角関数 角度 計算, 座標 角度 計算 エクセル, tan 角度 計算 エクセル, 勾配 角度 計算 エクセル, sin 角度 計算 エクセル,
0 件のコメント:
コメントを投稿